Poker Hands 5 Of A Kind
List the poker hand types for standard 5-card poker, straight flush, four of a kind, full house, flush, straight, three of a kind, two pair, pair, and nothing. For each hand type, show how to calculate the number of hands, give the number of hands, and find the probability for that hand type. 3-of-a-kind two pairs a pair high card Most poker games are based on 5-card poker hands so the ranking of these hands is crucial. There can be some interesting situations arising when the game involves choosing 5 cards from 6 or more cards, but in this case we are counting 5-card hands based on holding only 5 cards. The total number of 5-card. In poker, the probability of each type of 5-card hand can be computed by calculating the proportion of hands of that type among all possible hands. Frequency of 5-card poker hands The following enumerates the (absolute) frequency of each hand, given all combinations of 5 cards randomly drawn from a full deck of 52 without replacement.
Knowing what beats what in poker or Texas Hold’em is an important early step in learning the game. To help you out, I have provided for you an attractive printable or downloadable “cheat sheet” for both 5 card hand rankings as well as top 24 pre-flop starting hands.
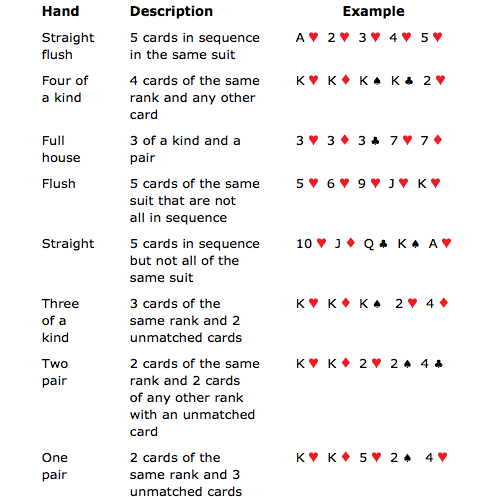
Poker hands ranked from best to worst:
- Royal Flush
- Straight Flush
- Four of a Kind
- Full House
- Flush
- Straight
- Three of a Kind
- Two Pair
- One Pair
- High Card
To make things easier on you, I have included some handy charts that can be used to reference during play or even printed out.
Poker Hand Rankings Chart
Never forget what beats what again. Feel free to save this to your phone/tablet/computer or print the chart out.
Click below to download a high-quality PDF that includes a printable copy of both the showdown and pre-flop hand rankings.
The Top 24 Hold’Em Starting Hand Rankings
To help you out, I have also included the top 24 no-limit hold’em starting hands to give you a further idea of what beats what in poker. I based this list on both raw equities as well as post-flop playability.
I have used over 10 years of experience in both tournaments and cash games to compile this info. You get to benefit from my hard work!
How These Hands Were Determined
I took a look at a few of the pre-flop hand ranking charts out there and, while most appeared to get it right for the most part, there seemed to be something off.
The thing is, everyone always does pretty well on the top 5 or 6 hands. However, after that things get a bit murkier
So, what really matters when it comes to weighing hand strength? I decided to take a close look at the problem. Using the knowledge I’ve gained over the past few years, I tried to come up with a better way of codifying hand rankings.
Determining the Overall Playability of Each Hand
I decided to go about it from a logical standpoint. When deciding whether to play a hand or not, what are the factors a strong player considers before acting
So, I decided that there are basically two main factors to consider in determining the strength of a particular pre-flop hand. And, since equity is the tool we use to rank the value of hands I just had to figure out what type of equities matter most and then apply it to each factor
Once I was able to define which equities to consider, it just took a bit of math.
1. Pre-Flop Equity
The first equity I decided to factor in is a hand’s raw pre-flop equity. I mean, sometimes you need to get all-in before the flop, right?
Of course, some hands will get all-in more frequently than others but for the sake of simplicity, raw equity against a strong range will give us a decent enough metric to come up with a comparative ranking.
2. Post-Flop Equity
Secondly, we need to factor in how a hand does post-flop. There’s no doubt, that certain hands play much better after the flop than others.
To calculate how well a hand does after the flop I looked at what post-flop hands tend to get all-in most of the time in a post-flop scenario. This includes the strongest made hands, including top pair and better, as well as strong draws.
Once I was able to figure out what hands are likely to get all-in, I just had to figure out the equity of every hand versus that range on a random flop.
Compiling the Final List
Poker Hands With 5 Of A Kind
Doing these kinds of calculations by hand would be extremely difficult and time-consuming. Luckily, there is a software program called Cardrunner’s EV that does the math for me.
After I figured out both the raw pre-flop equity and the likely flop equity of each hand, I just used excel to average them. That data was used to compile the rankings.
Here are the final equity percentages:
Which Poker Starting Hand Ranges Should I Use?
Knowing which hands to open raise is important to your success. Don’t worry, I’ve got you covered.
Free Basic Poker Strategy Charts
I have built charts that provide you profitable opening ranges from every position. As a bonus, the charts also include what to do at every decision point possible for playing a 20 to 40 big blind stack
The guide will give you an excellent starting point for playing No-Limit Texas Hold’em and will get you off on the right foot by allowing you to play fundamentally sound poker right now!
FAQ
What if my opponent and I have the same hand at showdown ?
If more than one player has the same hand then you have to follow the tie-breaker rules to determine the winner.
If two or more players have a flush or straight
In the case where two players have a flush or straight, the person who has the highest card in their hand wins. For example, T9876 beats 76543.
If two or more players have a full house
In the case of multiple full houses, the player with the highest “trips” as part of their full house wins. For example, TTT22 beats 555AA.
What if two or more players have the same pair or two pair?
If multiple players have exactly the same two pair, the highest kicker is used to determine the winner. For example, JJ66Q beats JJ66T.
The same process is used for one-pair. The next highest kicker is used. If that is the same, you use the next highest kicker. So on and so forth until the tie is broken. For example, AAK85 beats AAK84.
Who wins if more than one person has the same high card?
Similarly to one pair and two-pair hands, you use the next highest kicker to determine the winner. You keep moving on to the next kicker until a winner is determined. For example, KT763 beats KT753.
Which is better, trips or two-pair?
Three of a kind beats two-pair. It also beats a pair and high card.
Which is better, a flush or a straight?
A flush beats a straight. It also beats three of a kind, two pair, a pair, and high card.
What is the worst hand in poker?
The worst hand against multiple players is 72 offsuit. The worst hand heads-up is 32o.
What are the odds of getting a Royal Flush in Texas Hold’em?
A royal flush is extremely rare. You can only expect to get a royal flush once every 650,000 hands. That doesn’t mean it’s guaranteed. Personally, I have played well over 5 million hands and have only had one royal using both cards.
Final Thoughts
I hope this article has helped you learn more about how hand rankings work in poker. If you want to learn about basic poker strategy, be sure to check out my detailed no-limit hold’em basic tutorial.
Sanderson M. Smith
Home About Sanderson Smith Writings and Reflections Algebra 2 AP Statistics Statistics/Finance Forum
Poker Hands Chart With 5 Of A Kind
In many forms of poker, one is dealt 5 cards from astandard deck of 52 cards. The number of different 5 -card pokerhands is
A wonderful exercise involves having students verify probabilitiesthat appear in books relating to gambling. For instance, inProbabilities in Everyday Life, by John D. McGervey, one findsmany interesting tables containing probabilities for poker and othergames of chance.
This article and the tables below assume the reader is familiarwith the names for various poker hands. In the NUMBER OF WAYS columnof TABLE 2 are the numbers as they appear on page 132 in McGervey'sbook. I have done computations to verify McGervey's figures. Thiscould be an excellent exercise for students who are studyingprobability.
There are 13 denominations (A,K,Q,J,10,9,8,7,6,5,4,3,2) in thedeck. One can think of J as 11, Q as 12, and K as 13. Since an acecan be 'high' or 'low', it can be thought of as 14 or 1. With this inmind, there are 10 five-card sequences of consecutive dominations.These are displayed in TABLE 1.
TABLE 1The following table displays computations to verify McGervey'snumbers. There are, of course , many other possible poker handcombinations. Those in the table are specifically listed inMcGervey's book. The computations I have indicated in the table doyield values that are in agreement with those that appear in thebook.
N = NUMBER OF WAYS listed by McGervey | |||
Straight flush | There are four suits (spades, hearts, diamond, clubs). Using TABLE 1,4(10) = 40. | ||
Four of a kind | (13C1)(48C1) = 624. Choose 1 of 13 denominations to get four cards and combine with 1 card from the remaining 48. | ||
Full house | (13C1)(4C3)(12C1)(4C2) = 3,744. Choose 1 denominaiton, pick 3 of 4 from it, choose a second denomination, pick 2 of 4 from it. | ||
Flush | (4C1)(13C5) = 5,148. Choose 1 suit, then choose 5 of the 13 cards in the suit. This figure includes all flushes. McGervey's figure does not include straight flushes (listed above). Note that 5,148 - 40 = 5,108. | ||
Straight | (4C1)5(10) = 45(10) = 10,240 Using TABLE 1, there are 10 possible sequences. Each denomination card can be 1 of 4 in the denomination. This figure includes all straights. McGervey's figure does not include straight flushes (listed above). Note that 10,240 - 40 = 10,200. | ||
Three of a kind | (13C1)(4C3)(48C2) = 58,656. Choose 1 of 13 denominations, pick 3 of the four cards from it, then combine with 2 of the remaining 48 cards. This figure includes all full houses. McGervey's figure does not include full houses (listed above). Note that 54,912 - 3,744 = 54,912. | ||
Exactly one pair, with the pair being aces. | (4C2)(48C1)(44C1)(40C1)/3! = 84,480. Choose 2 of the four aces, pick 1 card from remaining 48 (and remove from consider other cards in that denomination), choose 1 card from remaining 44 (and remove other cards from that denomination), then chose 1 card from the remaining 40. The division by 3! = 6 is necessary to remove duplication in the choice of the last 3 cards. For instance, the process would allow for KQJ, but also KJQ, QKJ, QJK, JQK, and JKQ. These are the same sets of three cards, just chosen in a different order. | ||
Two pairs, with the pairs being 3's and 2's. | McGervey's figure excludes a full house with 3's and 2's. (4C2)(4C1)(44C1) = 1,584. Choose 2 of the 4 threes, 2 of the 4 twos, and one card from the 44 cards that are not 2's or 3's. |
'I must complain the cards are ill shuffled 'til Ihave a good hand.'
-Swift, Thoughts on Various Subjects
Home About Sanderson Smith Writings and Reflections Algebra 2 AP Statistics Statistics/Finance Forum
Previous Page Print This Page
Copyright © 2003-2009 Sanderson Smith